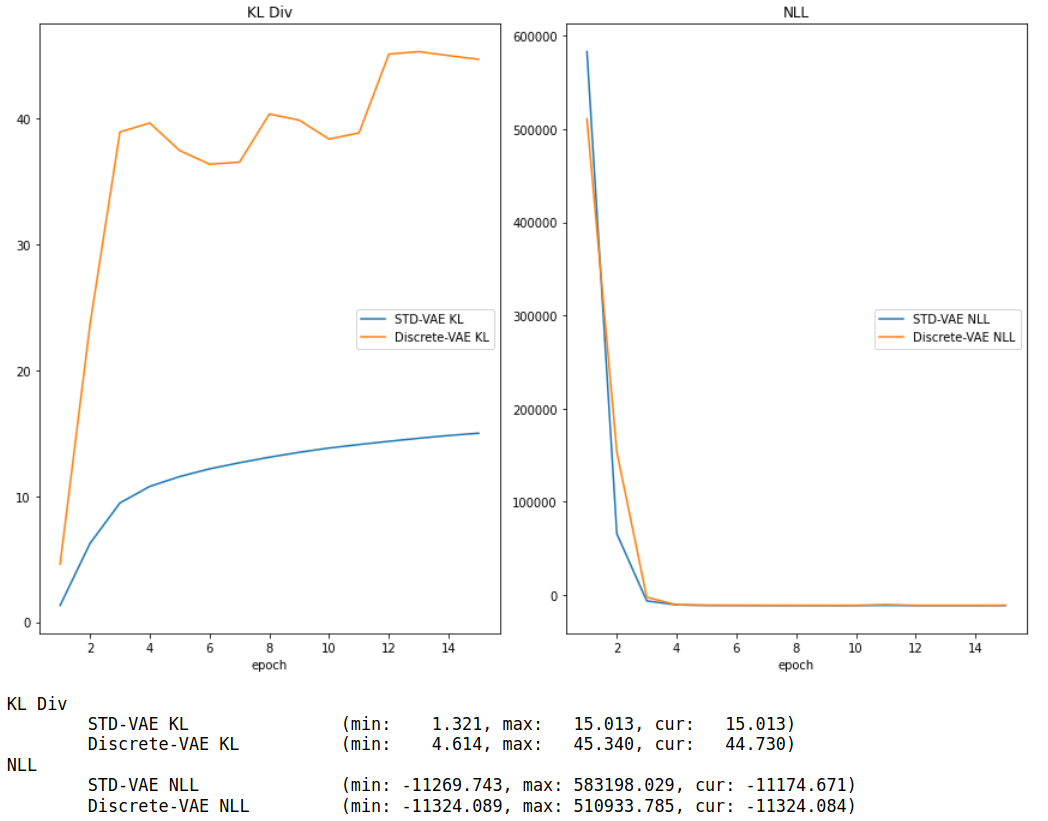
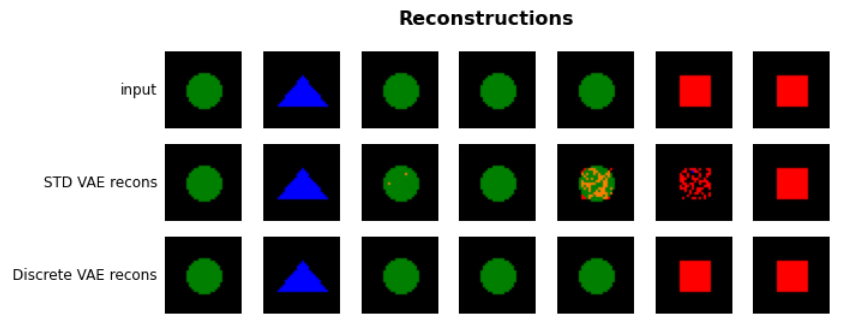
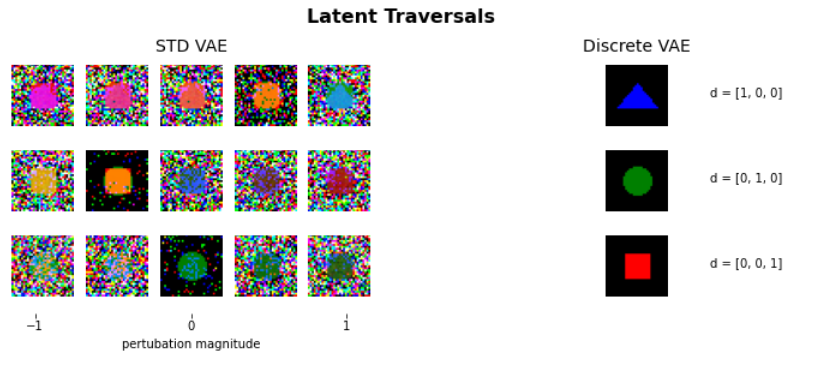
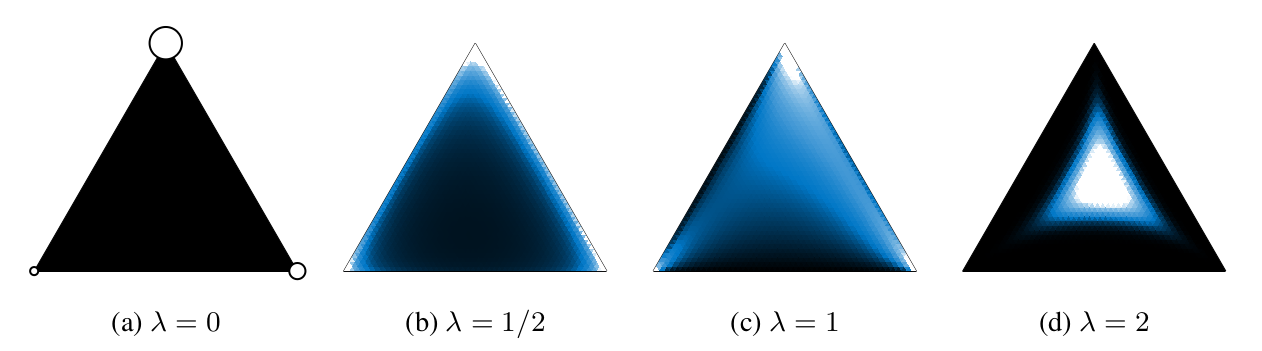The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables

reimplementation
VAE
D-VAE
Author

borea17

Published

February 21, 2021

Maddison et al. (2016) introduce CONtinuous relaxations of disCRETE (concrete) random variables as an approximation to discrete variables. The Concrete distribution is motivated by the fact that backpropagation through discrete random variables is not directly possible. While for continuous random variables, the reparametrization trick is applicable to allow gradients to flow through a sampling operation, this does not work for discrete variables due to the discontinuous operations associated to their sampling. The concrete distribution allows for a simple reparametrization through which gradients can propagate such that a low-variance biased gradient estimator of the discrete path can be obtained.

Model Description

The Concrete distribution builds upon the (very old) Gumbel-Max trick that allows for a reparametrization of a categorical distribution into a deterministic function over the distribution parameters and an auxiliary noise distribution. The problem within this reparameterization is that it relies on an \(\text{argmax}\)-operation such that backpropagation remains out of reach. Therefore, Maddison et al. (2016) propose to use the \(\text{softmax}\)-operation as a continuous relaxation of the \(\text{argmax}\). This idea has been concurrently developed at the same time by Jang et al. (2016) who called it the Gumbel-Softmax trick.

Gumbel-Max Trick

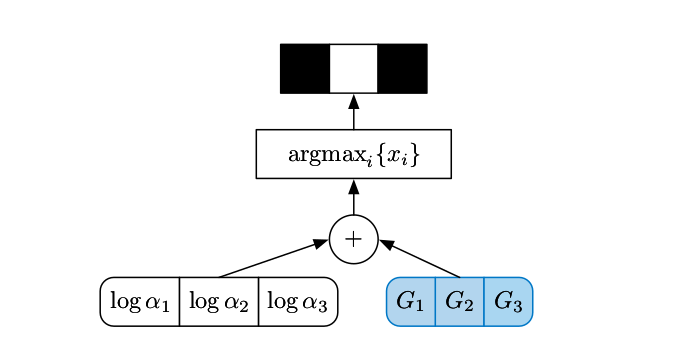
The Gumbel-Max trick basically refactors sampling of a deterministic random variable into a component-wise addition of the discrete distribution parameters and an auxiliary noise followed by \(\text{argmax}\), i.e.,

\[ \begin{align} \text{Sampling }&z \sim \text{Cat} \left(\alpha_1, \dots, \alpha_N \right) \text{ can equally expressed as } z = \arg\max_{k} \Big(\log\alpha_k + G_k\Big)\\ &\text{with } G_k \sim \text{Gumbel Distribution}\left(\mu=0, \beta=1 \right) \end{align} \]

Gumble Max
Computational Graph Gumbel-Max Trick. Taken from Maddison et al. (2016).

Derivation: Let’s take a closer look on how and why that works. Firstly, we show that samples from \(\text{Cat} \left(\alpha_1, \dots, \alpha_N \right)\) are equally distributed to

\[ z = \arg \min_{k} \frac {\epsilon_k}{\alpha_k} \quad \text{with} \quad \epsilon_k \sim \text{Exp}\left( 1 \right) \]

Therefore, we observe that each term inside the \(\text{argmin}\) is independent exponentially distributed with (easy proof)

\[ \frac {\epsilon_k}{\alpha_k} \sim \text{Exp} \Big( \alpha_k \Big) \]

The next step is to show that the index of the variable which achieves the minimum is distributed according to the categorical distribution (easy proof)

\[ \arg \min_{k} \frac {\epsilon_k}{\alpha_k} = P \left( k | z_k = \min \{ z_1, \dots, z_N \} \right) = \frac {\alpha_k}{\sum_{i=1}^N \alpha_i} \]

A nice feature of this formulation is that the categorical distribution parameters \(\{\alpha_i\}_{i=1}^N\) do not need to be normalized before reparameterization as normalization is ensured by the factorization itself. Lastly, we simply reformulate this mapping by applying the log and multiplying by minus 1

\[ z = \arg \min_{k} \frac {\epsilon_k}{\alpha_k} =\arg \min_k \Big(\log \epsilon_k - \log \alpha_k \Big) = \arg \max_k \Big(\log \alpha_k - \log \epsilon_k\Big) \]

This looks already very close to the Gumbel-Max trick defined above. Remind that to generate exponential distributed random variables, we can simply transform uniformly distributed samples of the unit interval as follows

\[ \epsilon_k = -\log u_k \quad \text{with} \quad u_k \sim \text{Uniform Distribution} \Big(0, 1\Big) \]

Thus, we get that

\[ - \log \epsilon_k = - \log \Big( - \log u_k \Big) = G_k \sim \text{Gumbel Distribution} \Big( \mu=0, \beta=1 \Big) \]

Gumbel-Softmax Trick

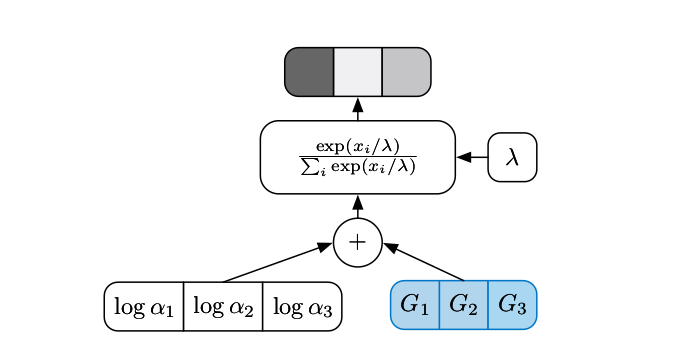
The problem in the Gumbel-Max trick is the \(\text{argmax}\)-operation as the derivative of \(\text{argmax}\) is 0 everywhere except at the boundary of state changes, where it is undefined. Thus, Maddison et al. (2016) use the temperature-valued \(\text{Softmax}\) as a continuous relaxation of the \(\text{argmax}\) computation such that

\[ \begin{align} \text{Sampling }&z \sim \text{Cat} \left(\alpha_1, \dots, \alpha_N \right) \text{ is relaxed cont. to } z_k = \frac {\exp \left( \frac {\log \alpha_k + G_k}{\lambda} \right)} {\sum_{i=1}^N \exp \left( \frac {\log \alpha_i + G_i}{\lambda} \right)}\\ &\text{with } G_k \sim \text{Gumbel Distribution}\left(\mu=0, \beta=1 \right) \end{align} \]

where \(\lambda \in [0, \infty[\) is the temperature and \(\alpha_k \in [0, \infty[\) are the categorical distribution parameters. The temperature can be understood as a hyperparameter that controls the sharpness of the \(\text{softmax}\), i.e., how much the winner-takes-all dynamics of the softmax is taken:

  • \(\lambda \rightarrow 0\): \(\text{softmax}\) smoothly approaches discrete \(\text{argmax}\) computation
  • \(\lambda \rightarrow \infty\): \(\text{softmax}\) leads to uniform distribution.

Note that the samples \(z_k\) obtained by this reparameterization follow a new family of distributions, the Concrete distribution. Thus, \(z_k\) are called Concrete random variables.

Gumble Softmax
Computational Graph Gumbel-Softmax Trick. Taken from Maddison et al. (2016).

Intuition: To better understand the relationship between the Concrete distribution and the discrete categorical distribution, let’s look on an exemplary result. Remind that the \(\text{argmax}\) operation for a \(n\)-dimensional categorical distribution returns states on the vertices of the simplex

\[ \boldsymbol{\Delta}^{n-1} = \left\{ \textbf{x}\in \{0, 1\}^n \mid \sum_{k=1}^n x_k = 1 \right\} \]

Concrete random variables are relaxed to return states in the interior of the simplex

\[ \widetilde{\boldsymbol{\Delta}}^{n-1} = \left\{ \textbf{x}\in [0, 1]^n \mid \sum_{k=1}^n x_k = 1 \right\} \]

The image below shows how the distribution of concrete random variables changes for an exemplary discrete categorical distribution \((\alpha_1, \alpha_2, \alpha_3) = (2, 0.5, 1)\) and different temperatures \(\lambda\).

Relationship between Concrete and Discrete Variables
Relationship between Concrete and Discrete Variables: A discrete distribution with unnormalized probabilities \((\alpha_1, \alpha_2, \alpha_3) = (2, 0.5, 1)\) and three corresponding Concrete densities at increasing temperatures \(\lambda\).
Taken from Maddison et al. (2016).

Concrete Distribution

While the Gumbel-Softmax trick defines how to obtain samples from a Concrete distribution, Maddison et al. (2016) provide a definition of its density and prove some nice properties:

Definition: The Concrete distribution \(\text{X} \sim \text{Concrete}(\boldsymbol{\alpha}, \lambda)\) with temperature \(\lambda \in [0, \infty[\) and location \(\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 & \dots & \alpha_n \end{bmatrix} \in [0, \infty]^{n}\) has a density

\[ p_{\boldsymbol{\alpha}, \lambda} (\textbf{x}) = (n-1)! \lambda^{n-1} \prod_{k=1}^n \left( \frac {\alpha_k x_k^{-\lambda - 1}} {\sum_{i=1}^n \alpha_i x_i^{-\lambda}} \right) \]

Nice Properties and their Implications:

  1. Reparametrization: Instead of sampling directly from the Concrete distribution, one can obtain samples by the following deterministic (\(d\)) reparametrization

    \[ X_k \stackrel{d}{=} \frac {\exp \left( \frac {\log \alpha_k + G_k}{\lambda} \right)} {\sum_{i=1}^N \exp \left( \frac {\log \alpha_i + G_i}{\lambda} \right)} \quad \text{with} \quad G_k \sim \text{Gumbel}(0, 1) \]

    This property ensures that we can easily compute unbiased low-variance gradients w.r.t. the location parameters \(\boldsymbol{\alpha}\) of the Concrete distribution.

  2. Rounding: Rounding a Concrete random variable results in the discrete random variable whose distribution is described by the logits \(\log \alpha_k\)

    \[ P (\text{X}_k > \text{X}_i \text{ for } i\neq k) = \frac {\alpha_k}{\sum_{i=1}^n \alpha_i} \]

    This property again indicates the close relationship between concrete and discrete distributions.

  3. Convex eventually:

    \[ \text{If } \lambda \le \frac {1}{n-1}, \text{ then } p_{\boldsymbol{\alpha}, \lambda} \text{ is log-convex in } x \]

    This property basically tells us if \(\lambda\) is small enough, there are no modes in the interior of the probability simplex.

Discrete-Latent VAE

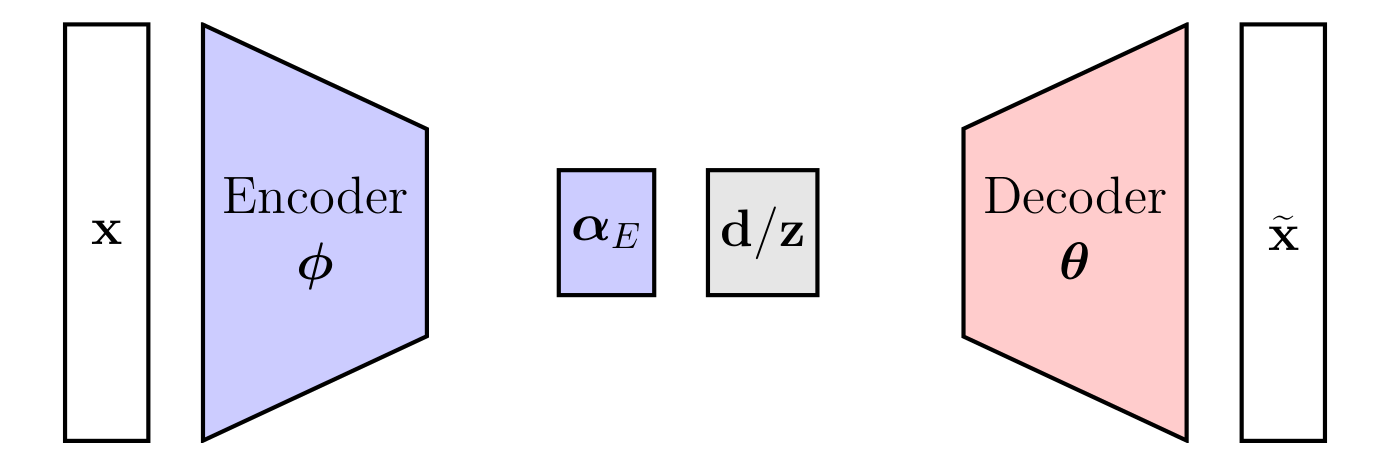
One use-case of the Concrete distribution and its reparameterization is the training of an variational autoencoder (VAE) with a discrete latent space. The main idea is to use the Concrete distribution during training and use discrete sampled latent variables at test-time. An obvious limitation of this approach is that during training non-discrete samples are returned such that our model needs to be able to handle continuous variables1. Let’s dive into the discrete-latent VAE described by Maddison et al. (2016).

We assume that we have a dataset \(\textbf{X} = \{\textbf{x}^{(i)}\}_{i=1}^N\) of \(N\) i.i.d. samples \(\textbf{x}^{(i)}\) which were generated by the following process:

  1. We sample a one-hot latent vector \(\textbf{d}\in\{0, 1\}^{K}\) from a categorical prior distribution \(P_{\boldsymbol{a}} (\textbf{d})\).
  2. We use our sample \(\textbf{d}^{(i)}\) and put it into the scene model \(p_{\boldsymbol{\theta}}(\textbf{x}|\textbf{d})\) from which we sample to generate the observed image \(\textbf{x}^{(i)}\).

As a result, the marginal likelihood of an image can be stated as follows

\[ p_{\boldsymbol{\theta}, \boldsymbol{a}} (\textbf{x}) = \mathbb{E}_{\textbf{d} \sim P_{\boldsymbol{a}}(\textbf{d})} \Big[ p_{\boldsymbol{\theta}} (\textbf{x} | \textbf{d}) \Big] = \sum P_{\boldsymbol{a}} \left(\textbf{d}^{(i)} \right) p_{\boldsymbol{\theta}} \left( \textbf{x} | \textbf{d}^{(i)} \right), \]

where the sum is over all possible \(K\) dimensional one-hot vectors. In order to recover this generative process, we introduce a variational approximation \(Q_{\boldsymbol{\phi}} (\textbf{d}|\textbf{x})\) of the true, but unknown posterior. Now we exchange the sampling distribution towards this approximation

\[ p_{\boldsymbol{\theta}, \boldsymbol{a}} (\textbf{x}) = \sum \frac {p_{\boldsymbol{\theta}, \boldsymbol{a}} \left(\textbf{x}, \textbf{d}^{(i)} \right)}{Q_{\boldsymbol{\phi}} \left(\textbf{d}^{(i)} | \textbf{x}\right)} Q_{\boldsymbol{\phi}} \left(\textbf{d}^{(i)} | \textbf{x}\right) = \mathbb{E}_{\textbf{d} \sim Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \left[ \frac {p_{\boldsymbol{\theta}, \boldsymbol{a}} \left(\textbf{x}, \textbf{d} \right)}{Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \right] \]

Lastly, applying Jensen’s inequality on the log-likelihood leads to the evidence lower bound (ELBO) objective of VAEs

\[ \log p_{\boldsymbol{\theta}, \boldsymbol{a}} (\textbf{x}) = \log \left( \mathbb{E}_{\textbf{d} \sim Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \left[ \frac {p_{\boldsymbol{\theta}, \boldsymbol{a}} \left(\textbf{x}, \textbf{d} \right)}{Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \right]\right) \ge \mathbb{E}_{\textbf{d} \sim Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \left[ \log \frac {p_{\boldsymbol{\theta}, \boldsymbol{a}} \left(\textbf{x}, \textbf{d} \right)}{Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \right] = \mathcal{L}^{\text{ELBO}} \]

While we are able to compute this objective, we cannot simply optimize it using standard automatic differentiation (AD) due to the discrete sampling operations. The concrete distribution comes to rescue: Maddison et al. (2016) propose to relax the terms \(P_{\boldsymbol{a}}(\textbf{d})\) and \(Q_{\boldsymbol{\phi}}(\textbf{d}|\textbf{x})\) using concrete distributions instead, leading to the relaxed objective

\[ \mathcal{L}^{\text{ELBO}}= \mathbb{E}_{\textbf{d} \sim Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \left[ \log \frac {p_{\boldsymbol{\theta}} \left(\textbf{x}| \textbf{d} \right) P_{\boldsymbol{a}} (\textbf{d}) }{Q_{\boldsymbol{\phi}} \left(\textbf{d} | \textbf{x}\right)} \right] \stackrel{\text{relax}}{\rightarrow} \mathbb{E}_{\textbf{z} \sim q_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{x}\right)} \left[ \log \frac {p_{\boldsymbol{\theta}} \left(\textbf{x}| \textbf{z} \right) p_{\boldsymbol{a}, \lambda_2} (\textbf{z}) }{q_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{x}\right)} \right] \]

Then, during training we optimize the relaxed objective while during test time we evaluate the original objective including discrete sampling operations. The really neat thing here is that switching between the two modes works out of the box: we only need to switch between the \(\text{softmax}\) and \(\text{argmax}\) operations.

Discrete-Latent VAE Architecture
Discrete-Latent VAE Architecture

Things to beware of: Maddison et al. (2016) noted that naively implementing [the relaxed objective] will result in numerical issues. Therefore, they give some implementation hints in Appendix C:

  • Log-Probabilties of Concrete Variables can suffer from underflow: Let’s investigate why this might happen. The log-likelihood of a concrete variable \(\textbf{z}\) is given by

    \[ \begin{align} \log p_{\boldsymbol{\alpha}, \lambda} (\textbf{z}) =& \log \Big((K-1)! \Big) + (K-1) \log \lambda + \left(\sum_{i=1}^K \log \alpha_i + (-\lambda - 1) \log z_i \right) \\ &- K \log \left(\sum_{i=1}^K \exp\left( \log \alpha_i - \lambda \log z_i\right)\right) \end{align} \]

    Now let’s remind that concrete variables are pushing towards one-hot vectors (when \(\lambda\) is set accordingly), i.e., due to rounding/underflow we might get some \(z_i=0\). This is problematic, since the \(\log\) is not defined in this case.

    To circumvent this, Maddison et al. (2016) propose to work with Concrete random variables in log-space, i.e., to use the following reparameterization

    \[ y_i = \frac {\log \alpha_i + G_i}{\lambda} - \log \left( \sum_{i=1}^K \exp \left( \frac {\log \alpha_i + G_i}{\lambda} \right) \right) \quad G_i \sim \text{Gumbel}(0, 1) \]

    The resulting random variable \(\textbf{y}\in\mathbb{R}^K\) has the property that \(\exp(Y) \sim \text{Concrete}\left(\boldsymbol{\alpha}, \lambda \right)\), therefore they denote \(Y\) as an \(\text{ExpConcrete}\left(\boldsymbol{\alpha}, \lambda\right)\). Accordingly, the log-likelihood \(\log \kappa_{\boldsymbol{\alpha}, \lambda}\) of a variable ExpConcrete variable \(\textbf{y}\) is given by

    \[ \begin{align} \log p_{\boldsymbol{\alpha}, \lambda} (\textbf{y}) =& \log \Big((K-1)! \Big) + (K-1) \log \lambda + \left(\sum_{i=1}^K \log \alpha_i + (\lambda - 1) y_i \right) \\ &- n \log \left(\sum_{i=1}^n \exp\left( \log \alpha_i - \lambda y_i\right)\right) \end{align} \]

    This reparameterization does not change our approach due to the fact that the KL terms of a variational loss are invariant under invertible transformations, i.e., since \(\exp\) is invertible, the KL divergence between two \(\text{ExpConcrete}\) is the same the KL divergence between two \(\text{Concrete}\) distributions.

  • Working with \(\text{ExpConcrete}\) random variables: Remind the relaxed objective

    \[ \mathcal{L}^{\text{ELBO}}_{rel} = \mathbb{E}_{\textbf{z} \sim q_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{x}\right)} \left[ \log p_{\boldsymbol{\theta}} \left( \textbf{x} | \textbf{z}\right) + \log \frac{ p_{\boldsymbol{a}, \lambda_2} (\textbf{z}) } {q_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{x}\right)} \right] \]

    Now let’s exchange the \(\text{Concrete}\) by \(\text{ExpConcrete}\) distributions

    \[ \mathcal{L}^{\text{ELBO}}_{rel} = \mathbb{E}_{\textbf{y} \sim \kappa_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{x}\right)} \left[ \log p_{\boldsymbol{\theta}} \left( \textbf{x} | \exp(\textbf{y})\right) + \log \frac{ \rho_{\boldsymbol{a}, \lambda_2} (\textbf{y}) } {\kappa_{\boldsymbol{\phi}, \lambda_1} \left(\textbf{z} | \textbf{y}\right)} \right], \]

    where \(\rho_{\boldsymbol{a}, \lambda_2} (\textbf{y})\) is the density of an \(\text{ExpConcrete}\) corresponding to the \(\text{Concrete}\) distribution \(p_{\boldsymbol{a}, \lambda_2} (\textbf{z})\). Thus, during the implementation we will simply use \(\text{ExpConcrete}\) random variables \(\textbf{y}\) as random variables and then perform an \(\exp\) computation before putting them through the decoder.

  • Choosing the temperature \(\lambda\): Maddison et al. (2016) note that the success of the training heavily depends on the choice of temperature. It is rather intuitive that the relaxed nodes should not be able to represent precise real valued mode in the interior of the probability simplex, since otherwise the model is designed to fail. In other words, the only modes of the concrete distributions should be at the vertices of the probability simplex. Fortunately, Maddison et al. (2016) proved that

    \[ \text{If } \lambda \le \frac {1}{n-1}, \text{ then } p_{\boldsymbol{\alpha}, \lambda} \text{ is log-convex in } x \]

    In other words, if we keep \(\lambda \le \frac {1}{n-1}\), there are no modes in the interior. However, Maddison et al. (2016) note that in practice, this upper-bound on \(\lambda\) might be too tight, e.g., they found for \(n=4\) that \(\lambda=1\) was the best temperature and in \(n=8\), \(\lambda=\frac {2}{3}\). As a result, they recommend to rather explore \(\lambda\) as tuneable hyperparameters.

    Last note about the temperature \(\lambda\): They found that choosing different temperatures \(\lambda_1\) and \(\lambda_2\) for the posterior \(\kappa_{\boldsymbol{\alpha}, \lambda_1}\) and prior \(\rho_{\boldsymbol{a}, \lambda_2}\) could dramatically improve the results.

Implementation

Let’s showcase how the discrete-latent VAE performs in comparison to the standard VAE (with Gaussian latents). For the sake of simplicity, I am going to create a very (VERY) simple dataset that should mimick the generative process we assume in the discrete-latent VAE, i.e., there are \(K\) one-hot vectors \(\textbf{d}\) and a Gaussian distribution \(p_{\boldsymbol{\theta}} (\textbf{x} | \textbf{d})\).

Data Generation

The dataset is made of three (\(K=3\)) distinct shapes each is assigned a distinct color such that in fact there are only three images in the dataset \(\textbf{X}=\{\textbf{x}_i\}_{i=1}^3\). Therefore, the Gaussian distribution \(p_{\boldsymbol{\theta}} (\textbf{x} | \textbf{d})\) has an infinitely small variance. To allow for minibatches during training and to make the epochs larger than one iteration, we upsample the three images by repeating each image \(1000\) times in the dataset:

Code 
import numpy as np
import torch
import torchvision.transforms as transforms
from PIL import Image, ImageDraw
from torch.utils.data import TensorDataset
from sklearn.preprocessing import OneHotEncoder


def generate_img(shape, color, img_size):
    """Generate an RGB image from the provided latent factors

    Args:
        shape (string): can only be 'circle', 'square', 'triangle'
        color (string): color name or rgb string
        img_size (int): describing the image size (img_size, img_size)
        size (int): size of shape

    Returns:
        torch tensor [3, img_size, img_size]
    """
    # blank image
    img = Image.new('RGB', (img_size, img_size), color='black')
    # center coordinates
    center = img_size//2
    # define coordinates
    x_0, y_0 = center - size//2, center - size//2
    x_1, y_1 = center + size//2, center + size//2
    # draw shapes
    img1 = ImageDraw.Draw(img)
    if shape == 'square':
        img1.rectangle([(x_0, y_0), (x_1, y_1)], fill=color)
    elif shape == 'circle':
        img1.ellipse([(x_0, y_0), (x_1, y_1)], fill=color)
    elif shape == 'triangle':
        y_0, y_1 = center + size//3,  center - size//3
        img1.polygon([(x_0, y_0), (x_1, y_0), (center, y_1)], fill=color)
    return transforms.ToTensor()(img)


def generate_dataset(n_samples_per_class, colors, shapes, sizes, img_size):
    data, labels = [], []
    for (n_samples, color, shape, size) in zip(n_samples_per_class,colors,shapes,sizes):
        img = generate_img(shape, color, img_size, size)

        data.append(img.unsqueeze(0).repeat(n_samples, 1, 1, 1))
        labels.extend(n_samples*[shape])
    # cast data to tensor [sum(n_samples_per_class), 3, img_size, img_size]
    data = torch.vstack(data).type(torch.float32)
    # create one-hot encoded labels
    labels = OneHotEncoder().fit_transform(np.array(labels).reshape(-1, 1)).toarray()
    # make tensor dataset
    dataset = TensorDataset(data, torch.from_numpy(labels))
    return dataset

IMG_SIZE = 32
N_SAMPLES_PER_CLASS = [1000, 1000, 1000]
SHAPES = ['square', 'circle', 'triangle']
COLORS = ['red', 'green', 'blue']
SIZES = [12, 14, 20]
dataset = generate_dataset(N_SAMPLES_PER_CLASS,COLORS, SHAPES, SIZES, IMG_SIZE)
Dataset
Dataset

Model Implementation

  • Standard VAE
Code 
import torch.nn as nn
import torch.distributions as dists

HIDDEN_DIM = 200
LATENT_DIM = 3
FIXED_VAR = 0.1**2


class VAE(nn.Module):

    def __init__(self):
        super(VAE, self).__init__()
        self.encoder = nn.Sequential(
            nn.Flatten(),
            nn.Linear((IMG_SIZE**2)*3, HIDDEN_DIM),
            nn.ReLU(),
            nn.Linear(HIDDEN_DIM, 2*LATENT_DIM)
        )
        self.decoder = nn.Sequential(
            nn.Linear(LATENT_DIM, HIDDEN_DIM),
            nn.ReLU(),
            nn.Linear(HIDDEN_DIM, (IMG_SIZE**2)*3),
        )
        return

    def compute_loss(self, x):
        [x_tilde, z, mu_z, log_var_z] = self.forward(x)
        # compute negative log-likelihood
        NLL = -dists.Normal(x_tilde, FIXED_VAR).log_prob(x).sum(axis=(1, 2, 3)).mean()
        # copmute kl divergence
        KL_Div = -0.5*(1 + log_var_z - mu_z.pow(2) - log_var_z.exp()).sum(1).mean()
        # compute loss
        loss = NLL + KL_Div
        return loss, NLL, KL_Div

    def forward(self, x):
        """feed image (x) through VAE

        Args:
            x (torch tensor): input [batch, img_channels, img_dim, img_dim]

        Returns:
            x_tilde (torch tensor): [batch, img_channels, img_dim, img_dim]
            z (torch tensor): latent space samples [batch, LATENT_DIM]
            mu_z (torch tensor): mean latent space [batch, LATENT_DIM]
            log_var_z (torch tensor): log var latent space [batch, LATENT_DIM]
        """
        z, mu_z, log_var_z = self.encode(x)
        x_tilde = self.decode(z)
        return [x_tilde, z, mu_z, log_var_z]

    def encode(self, x):
        """computes the approximated posterior distribution parameters and
        samples from this distribution

        Args:
            x (torch tensor): input [batch, img_channels, img_dim, img_dim]

        Returns:
            z (torch tensor): latent space samples [batch, LATENT_DIM]
            mu_E (torch tensor): mean latent space [batch, LATENT_DIM]
            log_var_E (torch tensor): log var latent space [batch, LATENT_DIM]
        """
        # get encoder distribution parameters
        out_encoder = self.encoder(x)
        mu_E, log_var_E = torch.chunk(out_encoder, 2, dim=1)
        # sample noise variable for each batch and sample
        epsilon = torch.randn_like(log_var_E)
        # get latent variable by reparametrization trick
        z = mu_E + torch.exp(0.5*log_var_E) * epsilon
        return z, mu_E, log_var_E

    def decode(self, z):
        """computes the Gaussian mean of p(x|z)

        Args:
            z (torch tensor): latent space samples [batch, LATENT_DIM]

        Returns:
            x_tilde (torch tensor): [batch, img_channels, img_dim, img_dim]
        """
        # get decoder distribution parameters
        x_tilde = self.decoder(z).view(-1, 3, IMG_SIZE, IMG_SIZE)
        return x_tilde

    def create_latent_traversal(self, image_batch, n_pert, pert_min_max=2, n_latents=3):
        device = image_batch.device
        # initialize images of latent traversal
        images = torch.zeros(n_latents, n_pert, *image_batch.shape[1::])
        # select the latent_dims with lowest variance (most informative)
        [x_tilde, z, mu_z, log_var_z] = self.forward(image_batch)
        i_lats = log_var_z.mean(axis=0).sort()[1][:n_latents]
        # sweep for latent traversal
        sweep = np.linspace(-pert_min_max, pert_min_max, n_pert)
        # take first image and encode
        [z, mu_E, log_var_E] = self.encode(image_batch[0:1])
        for latent_dim, i_lat in enumerate(i_lats):
            for pertubation_dim, z_replaced in enumerate(sweep):
                # copy z and pertubate latent__dim i_lat
                z_new = z.detach().clone()
                z_new[0][i_lat] = z_replaced

                img_rec = self.decode(z_new.to(device)).squeeze(0).cpu()

                images[latent_dim][pertubation_dim] = img_rec
        return images

  • Discrete-Latent VAE:

    Luckily, Pytorch distributions have already implemented the concrete distribution which even takes care of using the \(\text{ExpConcrete}\) for the computation of the log probability, see source code.

    As suggested by Maddison et al. (2016), we set \(\lambda_1 = \frac{2}{3}\). Setting \(\lambda_2 = 2\) seemed to improve stability, however I did not take time to really tune these hyperparameters (which is just not necessary due to the simplicity of the task).

Code 
LAMBDA_1 = torch.tensor([2/3])
LAMBDA_2 = torch.tensor([2.])
PRIOR_PROBS = 1/LATENT_DIM*torch.ones(LATENT_DIM)


class DiscreteVAE(nn.Module):

    def __init__(self):
        super(DiscreteVAE, self).__init__()
        self.encoder = nn.Sequential(
            nn.Flatten(),
            nn.Linear((IMG_SIZE**2)*3, HIDDEN_DIM),
            nn.ReLU(),
            nn.Linear(HIDDEN_DIM, LATENT_DIM)
        )
        self.decoder = nn.Sequential(
            nn.Linear(LATENT_DIM, HIDDEN_DIM),
            nn.ReLU(),
            nn.Linear(HIDDEN_DIM, (IMG_SIZE**2)*3),
        )
        self.register_buffer("LAMBDA_1", LAMBDA_1)
        self.register_buffer("LAMBDA_2", LAMBDA_2)
        self.register_buffer("PRIOR_PROBS", PRIOR_PROBS)
        return

    def compute_loss(self, x):
        [x_tilde, z, latent_dist] = self.forward(x, "Train")
        # compute negative log-likelihood
        NLL = -dists.Normal(x_tilde, FIXED_VAR).log_prob(x).sum(axis=(1, 2, 3)).mean()
        # copmute kl divergence
        PRIOR_DIST = dists.RelaxedOneHotCategorical(self.LAMBDA_2, self.PRIOR_PROBS)
        KL_Div =  (latent_dist.log_prob(z) - PRIOR_DIST.log_prob(z)).mean()
        # compute loss
        loss = NLL + KL_Div
        return loss, NLL, KL_Div

    def forward(self, x, mode="Train"):
        latent_dist, z = self.encode(x, mode)
        x_tilde = self.decode(z)
        return [x_tilde, z, latent_dist]

    def encode(self, x, mode="Train"):
        """computes the approximated posterior distribution parameters and
        returns the distribution (torch distribution) and a sample from that
        distribution

        Args:
            x (torch tensor): input [batch, img_channels, img_dim, img_dim]

        Returns:
            dist (torch distribution): latent distribution
        """
        # get encoder distribution parameters
        log_alpha = self.encoder(x)
        probs = log_alpha.exp()
        if mode == "Train":
            # concrete distribution
            latent_dist = dists.RelaxedOneHotCategorical(self.LAMBDA_1, probs)
            z = latent_dist.rsample()
            return [latent_dist, z]
        elif mode == "Test":
            # discrete distribution
            latent_dist = dists.OneHotCategorical(probs)
            d = latent_dist.sample()
            return [latent_dist, d]

    def create_latent_traversal(self):
        """in the discrete case there are only LATENT_DIM possible latent states"""
        # initialize images of latent traversal
        images = torch.zeros(LATENT_DIM, 3, IMG_SIZE, IMG_SIZE)
        latent_samples = torch.zeros(LATENT_DIM, LATENT_DIM)
        for i_lat in range(LATENT_DIM):
            d = torch.zeros(1, LATENT_DIM).to(self.LAMBDA_1.device)
            d[0][i_lat] = 1
            images[i_lat] = self.decode(d).squeeze(0)
            latent_samples[i_lat] = d
        return images, latent_samples

    def decode(self, z):
        """computes the Gaussian mean of p(x|z)

        Args:
            z (torch tensor): latent space samples [batch, LATENT_DIM]

        Returns:
            x_tilde (torch tensor): [batch, img_channels, img_dim, img_dim]
        """
        # get decoder distribution parameters
        x_tilde = self.decoder(z).view(-1, 3, IMG_SIZE, IMG_SIZE)
        return x_tilde
  • Training Procedure
Code 
from torch.utils.data import DataLoader
from livelossplot import PlotLosses

BATCH_SIZE = 128
LEARNING_RATE = 1e-3
WEIGHT_DECAY = 1e-6

def train(dataset, std_vae, discrete_vae, num_epochs):
    device = 'cuda' if torch.cuda.is_available() else 'cpu'
    print('Device: {}'.format(device))

    data_loader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True,
                             num_workers=12)
    std_vae.to(device)
    discrete_vae.to(device)

    optimizer_std_vae = torch.optim.Adam(std_vae.parameters(), lr=LEARNING_RATE,
                                         weight_decay=WEIGHT_DECAY)
    optimizer_dis_vae = torch.optim.Adam(discrete_vae.parameters(), lr=LEARNING_RATE,
                                         weight_decay=WEIGHT_DECAY)
    losses_plot = PlotLosses(groups={'KL Div': ['STD-VAE KL', 'Discrete-VAE KL'],
                                     'NLL': ['STD-VAE NLL', 'Discrete-VAE NLL']})
    for epoch in range(1, num_epochs + 1):
        avg_KL_STD_VAE, avg_NLL_STD_VAE = 0, 0
        avg_KL_DIS_VAE, avg_NLL_DIS_VAE = 0, 0
        for (x, label) in data_loader:
            x = x.to(device)
            # standard vae update
            optimizer_std_vae.zero_grad()
            loss, NLL, KL_Div  = std_vae.compute_loss(x)
            loss.backward()
            optimizer_std_vae.step()
            avg_KL_STD_VAE += KL_Div.item() / len(data_loader)
            avg_NLL_STD_VAE += NLL.item() / len(data_loader)
            # discrete vae update
            optimizer_dis_vae.zero_grad()
            loss, NLL, KL_Div  = discrete_vae.compute_loss(x)
            loss.backward()
            optimizer_dis_vae.step()
            avg_KL_DIS_VAE += KL_Div.item() / len(data_loader)
            avg_NLL_DIS_VAE += NLL.item() / len(data_loader)

        # plot current losses
        losses_plot.update({'STD-VAE KL': avg_KL_STD_VAE, 'STD-VAE NLL': avg_NLL_STD_VAE,
                            'Discrete-VAE KL': avg_KL_DIS_VAE,
                            'Discrete-VAE NLL': avg_NLL_DIS_VAE}, current_step=epoch)
        losses_plot.send()
    trained_std_vae, trained_discrete_vae = std_vae, discrete_vae
    return trained_std_vae, trained_discrete_vae

Results

Let’s train both models for some seconds:

Code 
num_epochs = 15
std_vae = VAE()
discrete_vae = DiscreteVAE()

trained_std_vae, trained_discrete_vae = train(dataset, std_vae, discrete_vae, num_epochs)

Training

Both models seem to be able to create descent reconstructions (really low NLL). From here on out, we will only run the discrete-latent VAE in test-mode, i.e., with a categorical latent distribution.

Visualizations

  • Reconstructions: Let’s verify that both models are able to create good reconstructions.
Code 
def plot_reconstructions(std_vae, discrete_vae, dataset, SEED=1):
    np.random.seed(SEED)
    device = 'cuda' if torch.cuda.is_available() else 'cpu'

    std_vae.to(device)
    discrete_vae.to(device)

    n_samples = 7
    i_samples = np.random.choice(range(len(dataset)), n_samples, replace=False)

    fig = plt.figure(figsize=(10, 4))
    plt.suptitle("Reconstructions", fontsize=16, y=1, fontweight='bold')
    for counter, i_sample in enumerate(i_samples):
        orig_img = dataset[i_sample][0]
        # plot original img
        ax = plt.subplot(3, n_samples, 1 + counter)
        plt.imshow(transforms.ToPILImage()(orig_img))
        plt.axis('off')
        if counter == 0:
            ax.annotate("input", xy=(-0.1, 0.5), xycoords="axes fraction",
                        va="center", ha="right", fontsize=12)
        # plot img reconstruction STD VAE
        [x_tilde, z, mu_z, log_var_z] = std_vae(orig_img.unsqueeze(0).to(device))

        ax = plt.subplot(3, n_samples, 1 + counter + n_samples)
        x_tilde = x_tilde[0].detach().cpu()
        plt.imshow(transforms.ToPILImage()(x_tilde))
        plt.axis('off')
        if counter == 0:
            ax.annotate("STD VAE recons", xy=(-0.1, 0.5), xycoords="axes fraction",
                        va="center", ha="right", fontsize=12)
        # plot img reconstruction IWAE
        [x_tilde, z, dist] = discrete_vae(orig_img.unsqueeze(0).to(device), "Test")
        ax = plt.subplot(3, n_samples, 1 + counter + 2*n_samples)
        x_tilde = x_tilde[0].detach().cpu()
        plt.imshow(transforms.ToPILImage()(x_tilde))
        plt.axis('off')
        if counter == 0:
            ax.annotate("Discrete VAE recons", xy=(-0.1, 0.5), xycoords="axes fraction",
                        va="center", ha="right", fontsize=12)
    return


plot_reconstructions(trained_std_vae, trained_discrete_vae, dataset)

Reconstructions

Interestingly, the standard VAE does not always create valid reconstructions. This is due to the sampling from a Gaussian in the latent space, i.e., the decoder might see some \(\textbf{z}\) it has not yet seen and then creates some weird reconstruction.

  • Latent Traversal: Let’s traverse the latent dimension to see what the model has learnt. Note that for the standard VAE the latent space is continuous and therefore infinitely many latent sample exist. As usual, we will only show an limited amount by pertubating each latent dimension between -1 and +1 (while holding the other dimensions constant).

    For the discrete-latent VAE, there are only \(K\) possible latent states.

Code 
def plot_latent_traversal(std_vae, discrete_vae, dataset, SEED=1):    
    np.random.seed(SEED)
    device = 'cuda' if torch.cuda.is_available() else 'cpu'
    
    std_vae.to(device)
    discrete_vae.to(device)
    
    n_samples = 1
    i_samples = np.random.choice(range(len(dataset)), n_samples, replace=False)
    img_batch = torch.cat([dataset[i][0].unsqueeze(0) for i in i_samples], 0)
    img_batch = img_batch.to(device)
    # generate latent traversals
    n_pert, pert_min_max, n_lats = 5, 1, 3
    img_trav_vae = std_vae.create_latent_traversal(img_batch, n_pert, pert_min_max, n_lats)
    img_discrete_vae, latent_samples = discrete_vae.create_latent_traversal()
    
    fig = plt.figure(figsize=(12, 5))
    n_rows, n_cols = n_lats + 1, 2*n_pert + 1
    gs = GridSpec(n_rows, n_cols)
    plt.suptitle("Latent Traversals", fontsize=16, y=1, fontweight='bold')
    for row_index in range(n_lats):
        for col_index in range(n_pert):
            img_rec_VAE = img_trav_vae[row_index][col_index]
            
            ax = plt.subplot(gs[row_index, col_index])
            plt.imshow(transforms.ToPILImage()(img_rec_VAE))
            plt.axis('off')
            
            if row_index == 0 and col_index == int(n_pert//2):
                plt.title('STD VAE', fontsize=14, y=1.1)
            
            ax = plt.subplot(gs[row_index, col_index + n_pert + 1])
            if col_index == 2:
                plt.imshow(transforms.ToPILImage()(img_discrete_vae[row_index]))
            if col_index == 3:
                d = latent_samples[row_index].type(torch.uint8).tolist()
                ax.annotate(f"d = {d}", xy=(0.5, 0.5))
                
            
            plt.axis('off')
            if row_index == 0 and col_index == int(n_pert//2):
                plt.title('Discrete VAE', fontsize=14, y=1.1)
            
            
    # add pertubation magnitude
    for ax in [plt.subplot(gs[n_lats, 0:5])]:
        ax.annotate("pertubation magnitude", xy=(0.5, 0.6), xycoords="axes fraction",
                    va="center", ha="center", fontsize=10)
        ax.set_frame_on(False)
        ax.axes.set_xlim([-1.15 * pert_min_max, 1.15 * pert_min_max])
        ax.xaxis.set_ticks([-pert_min_max, 0, pert_min_max])
        ax.xaxis.set_ticks_position("top")
        ax.xaxis.set_tick_params(direction="inout", pad=-16)
        ax.get_yaxis().set_ticks([])
    return

plot_latent_traversal(trained_std_vae, trained_discrete_vae, dataset)

Latent Traversal

Well, this looks nice for the discrete VAE and really confusing for the Standard VAE.

Acknowledgements

The lecture on discrete latent variables by Artem Sobolev as well as the NIPS presentation by Eric Jang were really helpful resources.

Footnotes

  1. While continuous variables do not pose a problem for standard VAEs with neural networks as approximations, it should be noted that there are numerous cases in which we cannot operate with continuous variables, e.g., when the (discrete) variable is used as a decision variable.↩︎